
本日は、ゲーム制作の技術的な内容について紹介してみたいと思います。
実際のカーナビにも使われている最短経路探索アルゴリズム、つまり、ある地点から目的地までどういうルートで行けば最短なのかを探す処理って、どう作られているのか気になったりしますよね?
まず、最短経路探索アルゴリズムが実際に使われている例としては、鉄道の経路案内やカーナビなどがあります。
ゲームでも、広いマップがあるゲームだとナビゲーションシステムとして最短経路探索アルゴリズムが動いています。
最近はオープンワールドを舞台としたゲームがたくさんあるので、このナビゲーションシステムは必須ですよね!
プレイヤーの道案内だけではなく、敵キャラクターがどのようなルートを辿れば目的地へ辿り着くことができるのかを計算するときにも使用します。
例えば、ゼルダの伝説のゴブリンがプレイヤーへ迫ってくるときのルートの計算にも使われており、かなり様々な場所で使われている技術です。
ちなみにこの技術を応用すれば、最短経路だけではなく、一番安全なルートを見つけることも可能になります。
広大なマップの中で、現在地から目的地までを一番短いルートで導いてくれるなんて、とても賢そうに見えますよね。
これは一種のAI(人工知能)で、ゲーム内の地図情報からうまいこと計算して最短ルートを導き出しています。
最短経路の求め方
3Dで表現された複雑なマップだと理解し難いので、分かりやすいようにタイル状のマップで説明します。
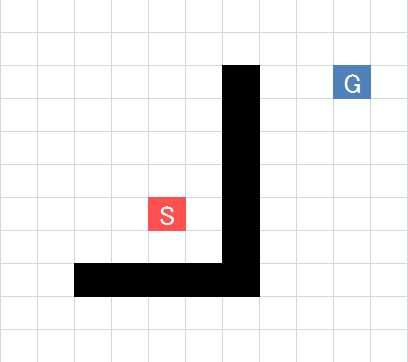
まず、上のように、S(スタート)とG(ゴール)が存在するマップがあります。
黒い部分は障害物で、通ることはできません。
スタート地点からゴール地点までの最短ルートを求めたいとします。
人間は、ぱっと見ただけで大体の答えが分かりますよね。以下のようになります。
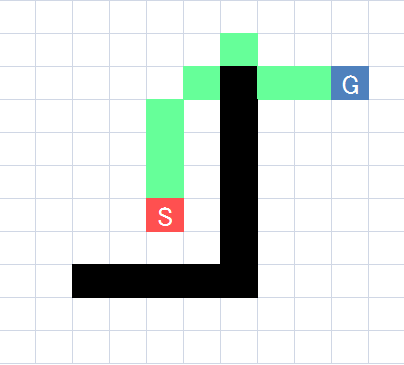
では、コンピューターはこれをどうやって求めているのでしょうか。
一番簡単なのは、スタート地点から全てのタイルへの移動距離を計算する方法です。
全てのタイルへの移動ルートが分かるので、当然ゴールまでの移動ルートも導出できるといった力技ですね。
コンピュータが最短経路を計算する手順
まずは、スタート地点から1つ移動するだけで辿り着けるタイルの場所を見つけます。
タイルに書かれている1というのが、何個分のタイルを移動したかという数字です。
次に、2つ移動するだけで辿り着けるタイルの場所を見つけ、次は3つ目・・・といった感じで、スタート地点を中心に移動できる範囲を広げていきます。
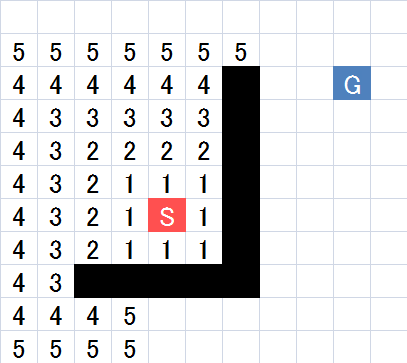
コスト5のタイルまで計算すると、こうなりますね。
これを全てのタイルが埋まるまで繰り返し行います。

こうなりました。
つまり、ゴール地点までは8つタイルを移動すれば辿り着くことができます。
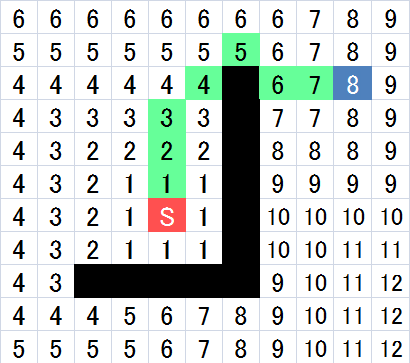
あとは、ゴール地点から8→7→6…というように数字が減るように遡っていけば、スタート地点からゴール地点までの最短ルートが導き出されます。
この場合、最短ルートは何通りかありますが、どれでも良さそうですね。
ゲームには使えない?
一応、これで求められますが…自分を中心にして全てのタイルへの移動コストを計算する必要があるので、これを最近のゲームのような広大なマップで計算すると、計算時間が大変なことになります。
また、プレイヤーからモンスターへの経路を求めたい場合は、多くの場合、その2つは常に動いているので、毎フレームでこの計算を行わなければならないことになり、とても現実的ではありませんよね。
なので、実際には、もっと高速に求められる方法が使われることや、計算結果を何フレームかに分けて計算する、計算結果を保存して使い回すなどの工夫がされています。
ちなみに、この計算方法はダイクストラのアルゴリズムと呼ばれるもので、ゲーム以外で最短経路を求めるときによく使われているようですが、ゲームだとリアルタイムで計算しなければならないのでほとんど使われていないようです。






















お気軽にコメントをどうぞ!